Continuum limit

The idea here is to consider the limit N→∞ and express this by using distributions of oscillators instead of discrete oscillators. We denote by ρ(θ,t,ω)

The normalization condition is that ∫2π0ρ(θ,t,ω)dθ=1.

Since the number of oscillators is conserved we can write a continuity equation which can be derived in the same way as the continuity equation for 1-dimensional fluids. The continuity equation is ∂ρ∂t+∂∂θ(ρυ)=0, where υ is the velocity of an oscillator with natural frequency ω and phase θ. Therefore, υ=˙θ=ω+Krsin(ψ−θ).

The order parameter can be written in terms of these distributions as reiψ=∫2π0∫∞−∞ρ(θ′,t,ω′)g(ω′)eiθ′dω′dθ′.

Therefore, rei(ψ−θ)=∫2π0∫∞−∞ρ(θ′,t,ω′)g(ω′)ei(θ′−θ)dω′dθ′, and we finally obtain by considering the imaginary parts that υ=ω+K∫2π0∫∞−∞ρ(θ′,t,ω′)g(ω′)sin(θ′−θ)dω′dθ′.

The full equation for the continuum limit of the Kuramoto model can then be written as

Stationary solutions

Stationary distributions do not change in time. Therefore, ∂ρ/∂t=0 and ∂∂θ(ρυ)=0, implying ρυ=C(ω). If C(ω)≠0, then ρ=C(ω)/υ. If C(ω)=0 then ρ is a delta-function at υ=0.

A stationary distribution is the uniform distribution ρ(θ,ω)=12π, which can be easily seen to satisfy the continuum limit Kuramoto equation and which corresponds to the incoherent state.

Perturbations of the incoherent state

Consider the perturbation of the incoherent state given by ρ(θ,t,ω)=12π+εη(θ,t,ω).

Exercise. Show that to first order in ε we have

We write a Fourier series for η as η(θ,t,ω)=∞∑n=1cn(t,ω)einθ+ˉcn(t,ω)e−inθ.

Then ∫2π0η(θ′,t,ω′)sin(θ′−θ)dθ′=−2πIm(c1eiθ).

Subsequently, we find that ∂c1∂t+iωc1−K2∫∞−∞c1(t,ω′)g(ω′)dω′=0,

and, for n≥2, ∂cn∂t+inωcn=0.

Therefore, for n≥2 we immediately obtain cn(t,ω)=cn(0,ω)einωt.

For n=1 we consider the operator A given by Ac:=−iωc+K2∫∞−∞c(t,ω′)g(ω′)dω′, so that we can write ∂c1∂t=Ac1.

It turns out that the spectrum of A has a continuous part given by {iω:ω∈supp(g)}. Such eigenvalues imply neutral stability. If we only have eigenvalues on the imaginary axis then the linear stability analysis is not sufficient to determine the stability of the solution.

We look for discrete eigenvalues of A through the ansatz c(t,ω)=b(ω)eλt.

Then λb=−iωb+K2∫∞−∞b(ω′)g(ω′)dω′. Let B=K2∫∞−∞b(ω′)g(ω′)dω′. Then b(ω)=Bλ+iω.

Therefore, we can write λBλ+iω=−iωBλ+iω+K2∫∞−∞Bλ+iω′g(ω′)dω′, implying 1=K2∫∞−∞g(ω′)λ+iω′dω′. We consider again a Lorentzian distribution g(ω)=γπ(ω2+γ2). Therefore, 1=K2∫∞−∞1λ+iωγπ(ω2+γ2)dω=Kγ2πi∫∞−∞1ω−iλ1ω2+γ2dω.

Using residues we find (closing the integration path with a half-circle on the upper-half complex plane) that for λ<0 we have the contradiction 1=KγRes(iγ)=K2(λ−γ)<0. For λ>0 we find (closing the integration path with a half-circle on the lower-half complex plane) 1=−KγRes(−iγ)=K2(λ+γ), giving λ=K2−γ=K−Kc2.

This shows that for K>Kc the incoherent state becomes unstable and small perturbations grow exponentially as ∼eK−Kc2t.

The Ott-Antonsen ansatz is a method that allows to find the time evolution of r(t) (the modulus of the order parameter) for special types of solutions of the Kuramoto model.

Recall that the full equation for the continuum limit of the Kuramoto model has the form

The left-hand side of the equation becomes

A Fourier series expansion of ρ gives ρ(θ,t,ω)=12π∞∑n=−∞cn(t,ω)einθ, where c−n=ˉcn and c0=1 (the last relation because of the normalization of ρ(θ,t,ω)).

Then we have reiψ=∫∞−∞dω′g(ω′)∫2π0dθ′ρ(θ′,t,ω′)eiθ′=∫∞−∞dω′g(ω′)(12π∞∑n=−∞cn(t,ω′)∫2π0dθ′einθ′eiθ′)=∫∞−∞dω′g(ω′)c−1(t,ω′)=∫∞−∞dω′g(ω′)ˉc1(t,ω′).

Substituting the Fourier series for ρ into the equation 0=∂ρ∂t+∂∂θ[ρ(ω+KIm(reiψe−iθ))]=∂ρ∂t+∂∂θ[ρ(ω+K2ireiψe−iθ−K2ire−iψeiθ)], we obtain the relation ∂cn∂t+in(ωcn+Kreiψ2icn+1−Kre−iψ2icn−1)=0.

The Ott-Antonsen ansatz is to consider distributions with cn(t,ω)=α(t,ω)n, for n≥1. Consequently, cn=ˉc|n|=ˉα|n| for n≤−1.

Then,

re−iψ=∫∞−∞dω′g(ω′)α(t,ω′),

and the equation for cn from the previous slide becomes

∂α∂t+iωα+Kre−iψ2[e2iψα2−1]=0.

We now compute the integral

re−iψ=∫∞−∞dω′g(ω′)α(t,ω′),

assuming that α is analytic in the lower half complex plane (as a function of a complexified ω).

Then, choosing a Lorentzian g(ω)=γ/(π(ω2+γ2)) we have

re−iψ=∫∞−∞dω′g(ω′)α(t,ω′)=−2πiRes(−iγ)=α(−iγ,t).

Setting ω=−iγ into the equation for α and using the relation between the order parameter and α(−iγ,t) we obtain

ddt(re−iψ)+γre−iψ+Kre−iψ2[r2−1]=0.

Then drdte−iψ−irdψdte−iψ+γre−iψ+Kre−iψ2[r2−1]=0, and drdt−irdψdt+γr+Kr2[r2−1]=0.

Therefore, we get two equations. The first one is r˙ψ=0 and the second one is drdt+γr+Kr2[r2−1]=0.

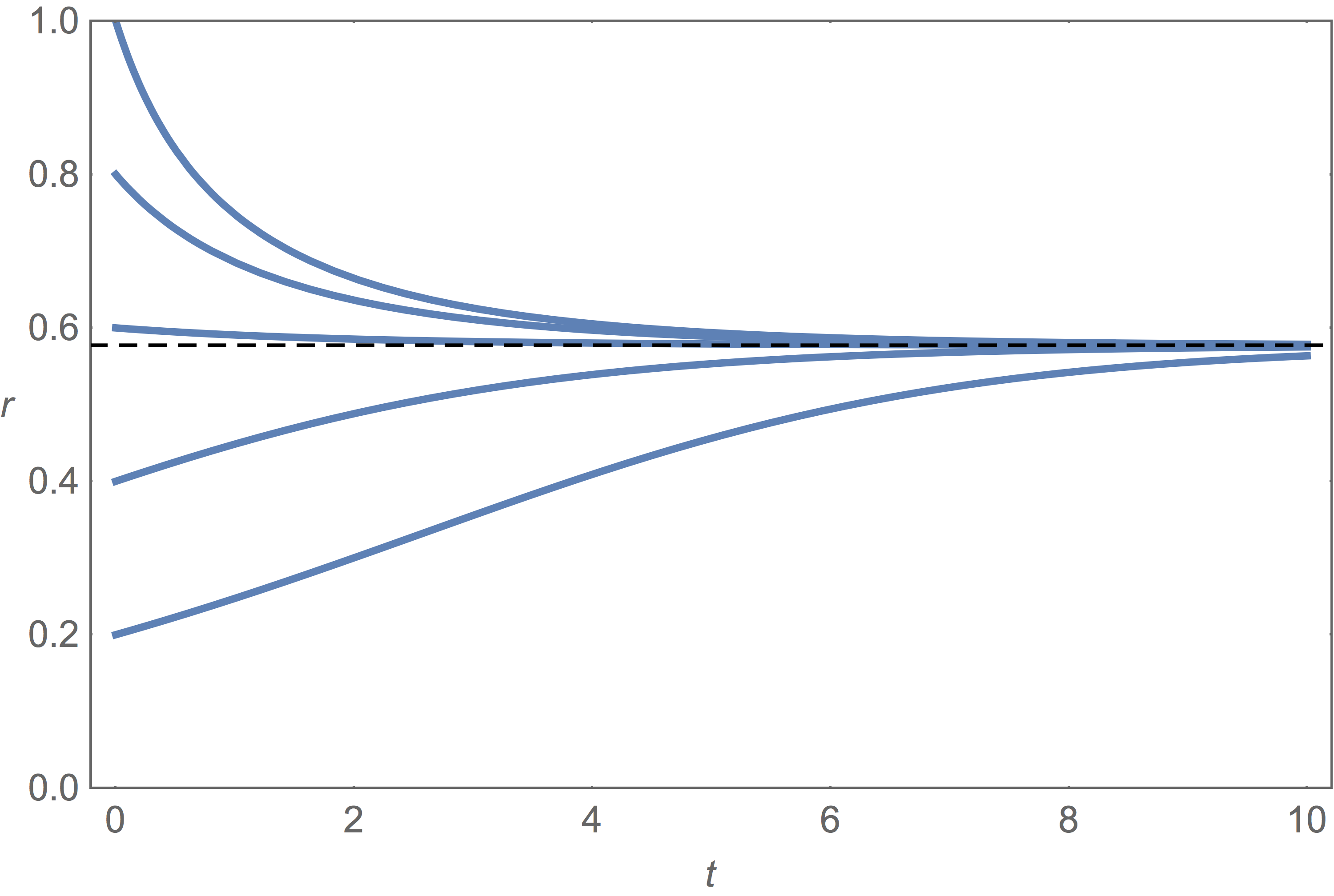
The equation drdt+γr+Kr2(r2−1)=0. has equilbria r=0 and r=√1−Kc/K. These can be found by solving the equation f(r)=−γr−Kr2(r2−1)=0.

For the linear stability we need to consider the linearization at the equilibria. This can be determined through the derivative at the equilibria. We have f′(r)=−γ+K2−3Kr22.

For the incoherent state, r=0, we get f′(0)=−γ+K2=K−Kc2, where Kc=2γ.

Therefore the incoherent state seems be stable if f′(0)<0 which implies K<Kc, and unstable if K>Kc.

For the second branch, given by r=r∗=√1−K/Kc for K>Kc, we have

f′(r∗)=−(K−Kc).

Therefore, this branch is stable for K>Kc (and it does not exist for K<Kc).

The equation for r, drdt+γr+Kr2(r2−1)=0, is separable and can be easily integrated. Nevertheless, the computations become easier making the substitution u=r2 which gives ˙u=2r˙r. Multiplying the previous equation by 2r we find 2rdrdt+2γr2+Kr2(r2−1)=0, which becomes dudt=−Kcu−Ku(u−1). Rearranging terms we find dudt=(K−Kc)u−Ku2,

and duKdt=(1−KcK)u−u2. Let δ=1−KcK. Then the equation becomes duKdt=δu−u2, which is a rewriting of the logistic equation.

Integration gives

1δln|uu−δ|=Kt, and then uu−δ=AeδKt=Ae(K−Kc)t.

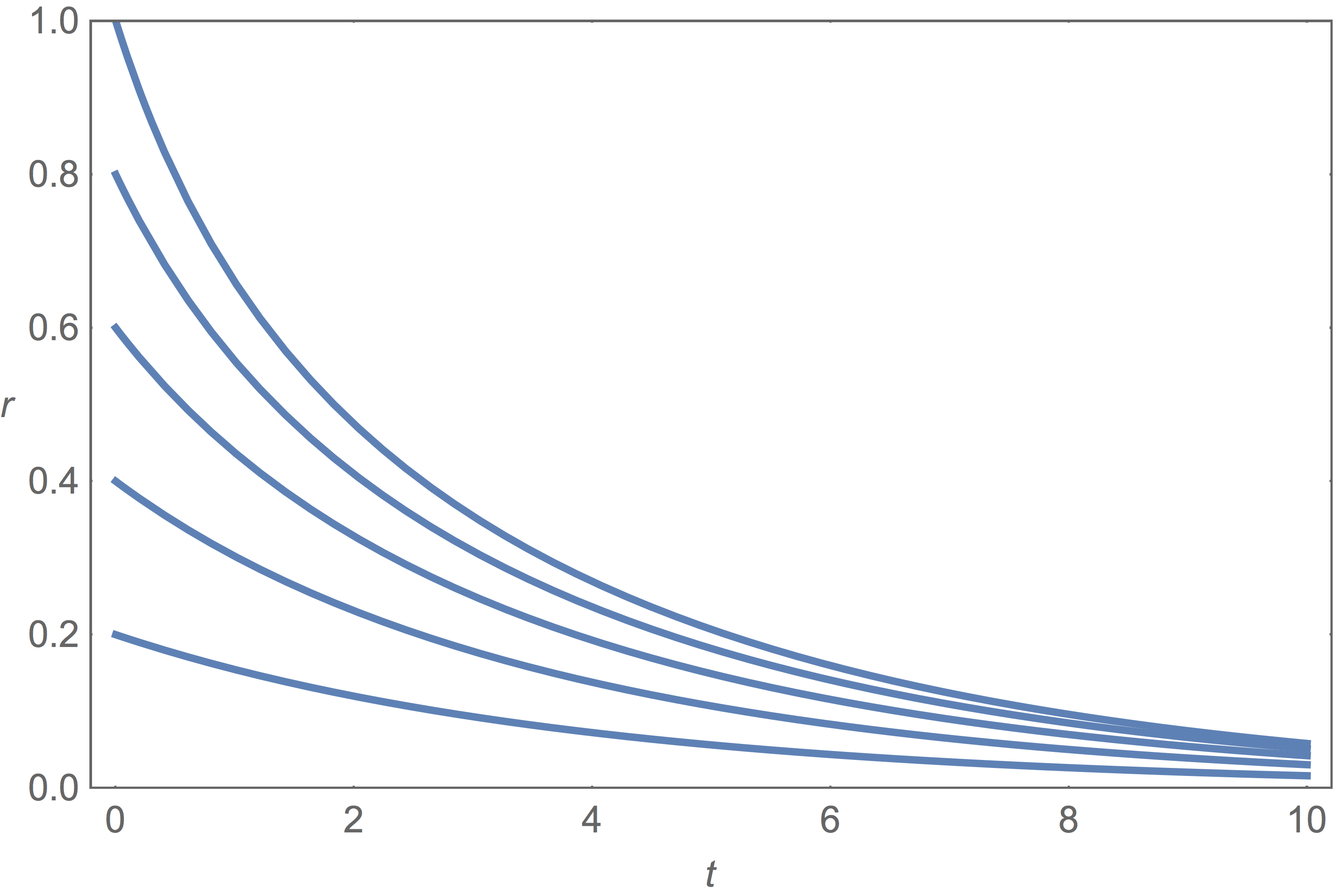
Solving for u we find u=δ1−1Ae−(K−Kc)t. Moreover, if for t=0 we have u=u0 we can write A=u0u0−δ, and we get u=δu0u0−(u0−δ)e−(K−Kc)t.

For t→∞ we find that if K−Kc<0 then u→0.

If Kδ>0 and u0≠0 then for t→∞ we find u→δ, implying r→√1−KcK. Finally, if u0=0 then u=0 for all t.