Global geometry of physical systems and its quantum manifestations

This article appeared in issue 2017-2 of Periodiek, the magazine of the FMF student association.

Looking at geometric properties of physical systems from a global point of view reveals a rich geometric structure which can be described using ideas from differential geometry and algebraic topology [1]. These geometric properties are relevant to physical systems as fundamental as the hydrogen atom and, even though they arise in the context of classical mechanics, they have significant implications for the corresponding quantum system.

To describe the main ideas that come into play in this research direction I will focus on the example of the spherical pendulum. At first sight, the spherical pendulum is not a very intriguing system. It is integrable, that is, the differential equations describing its motion can be solved in terms of known (but non-elementary) functions.¹ And you could reasonably ask, if we can find all motions, then don’t we know everything about the system? Well, not quite. Looking at individual motions is like looking through a microscope and may lead to missing the whole picture. There are questions related to global properties which can be answered only if we take a step back and look at the system from a more abstract point of view.

The integrability of the spherical pendulum is not just a happy accident. It has a much deeper reason, related to the existence of two conserved quantities,² the total energy

and the (vertical component of the) angular momentum

Here we are using spherical coordinates where $\theta \in [0,\pi ]$ is the inclination angle, $\varphi \in [0,2\pi ]$ is the azimuthal angle, and a dot denotes the corresponding time derivative. A very famous theorem in classical mechanics, the Liouville-Arnold theorem, states that the existence of these integrals (together with some technical conditions) implies that the system is integrable. Moreover, the same theorem allows us to make a first step toward a global description of an integrable system. Applied to the spherical pendulum, it states that for most choices of values of $(L,E)$ the points $(\theta ,\varphi ,\dot{\theta },\dot{\varphi })$ in phase space with the given $(L,E)$ form a torus $T^2$ (Figure 1). Consequently, all motions with these values $(L,E)$ lie on the same torus.

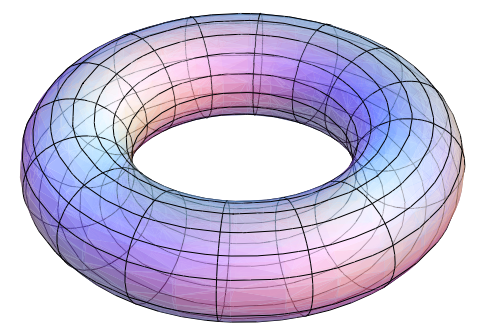
There are some exceptions to having tori. The most relevant one for this discussion is the unstable equilibrium, where the spherical pendulum is motionless at its topmost point with $\theta =0$, implying $(L=0,E=1)$. The set of all points in phase space with $(L=0,E=1)$ form a pinched torus (Figure 2). The bifurcation diagram (Figure 3) shows the values $(L,E)$ corresponding to tori (gray area), the exceptional value $P=(L=0,E=1)$ corresponding to the pinched torus, and other exceptional cases. This diagram and the associated information is something that one cannot easily deduce by staring at complicated algebraic expressions of the motions. Here, the general theory provides powerful tools to reach these conclusions through qualitative arguments.

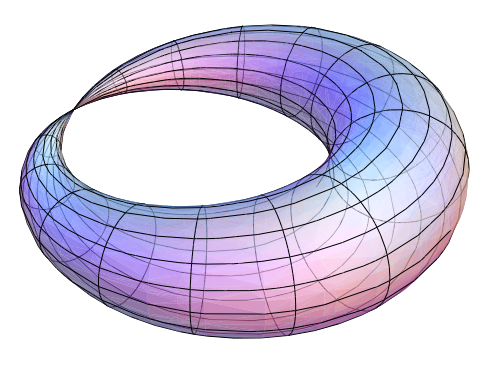
The next question from a geometric point of view, and a very natural one for a mathematician to ask, is how all the tori fit together. To understand this question, consider the well-known example of the cylinder and the Möbius band (Figure 4). Even though a cylinder and a Möbius band locally look identical, globally they are very different. Both can be obtained by considering a rectangle, and gluing two opposite sides of the rectangle in different ways.³ A consequence of gluing the sides differently is that the cylinder is the Cartesian product of a circle and an interval, while the Möbius band is non-orientable and cannot be written as a Cartesian product.

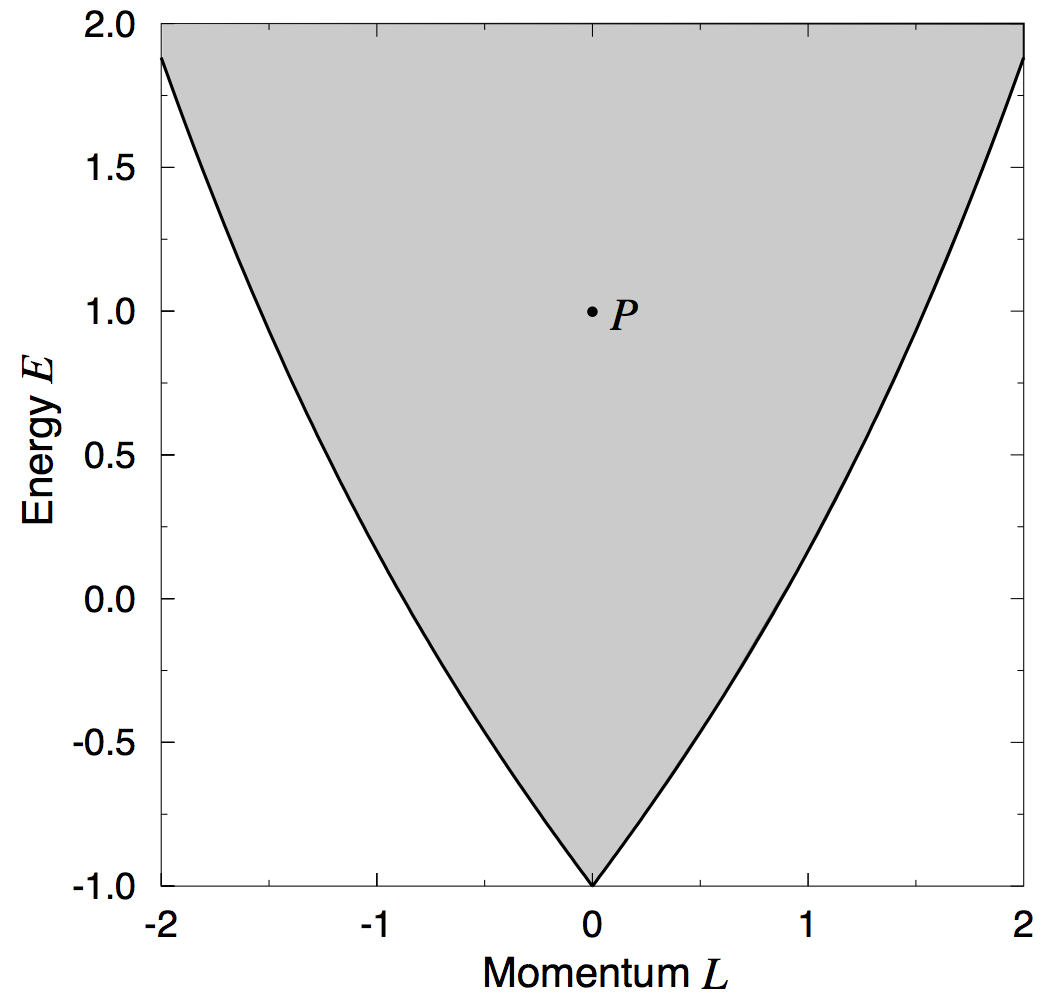
Back to the spherical pendulum, consider a loop $L$ in the gray area in Figure 3. Each point on the loop corresponds to a $T^2$ in phase space and taking all these tori together gives a bundle of tori over $\mathbf{L}$. Such bundles can be classified through a gluing map: start with the Cartesian product $[0,1]\times T^2$ and then glue the tori at the endpoints of $[0,1]$ to obtain the required bundle (Figure 5). The gluing is given by a $2\times 2$ integer matrix with determinant $\pm 1$, called monodromy matrix. The main observation is that the bundle of tori is a Cartesian product $L\times T^2$ if and only if the monodromy matrix is identity. In the spherical pendulum, it has been shown that the monodromy matrix for a loop $L$ going once around $P$ is

implying that in this case the bundle is not a Cartesian product and the tori are glued with a “twist”. We say that the spherical pendulum has non-trivial monodromy [2].

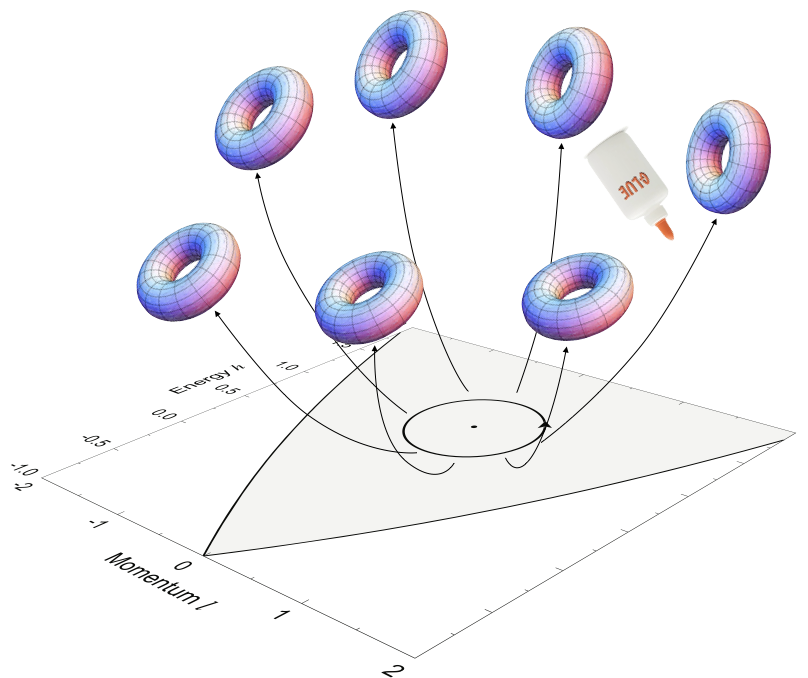
These are few of the things that one can say about the global geometry of the spherical pendulum and there are many more interesting connections that one can make with other deep geometric ideas. For example, we have recently shown that the reason for non-trivial monodromy is that a Hopf fibration is hidden in the neighborhood of the unstable equilibrium [3].

The non-trivial geometry of the spherical pendulum manifests in the corresponding quantum system. Here one can define the joint spectrum of the two quantum operators that correspond to the energy and the angular momentum (Figure 6). You can see in the joint spectrum that if you take a small cell and you move it along a loop going around $P$ you end up with a different cell than what you started with, a manifestation of quantum monodromy. And if you pay close attention to the difference between the sides of the initial and final cells you can even read the monodromy matrix from this picture! Quantum monodromy has been found in a wide variety of fundamental atomic and molecular systems, for example, the hydrogen atom [4,5], and is important for assigning quantum numbers to experimentally observed spectra.

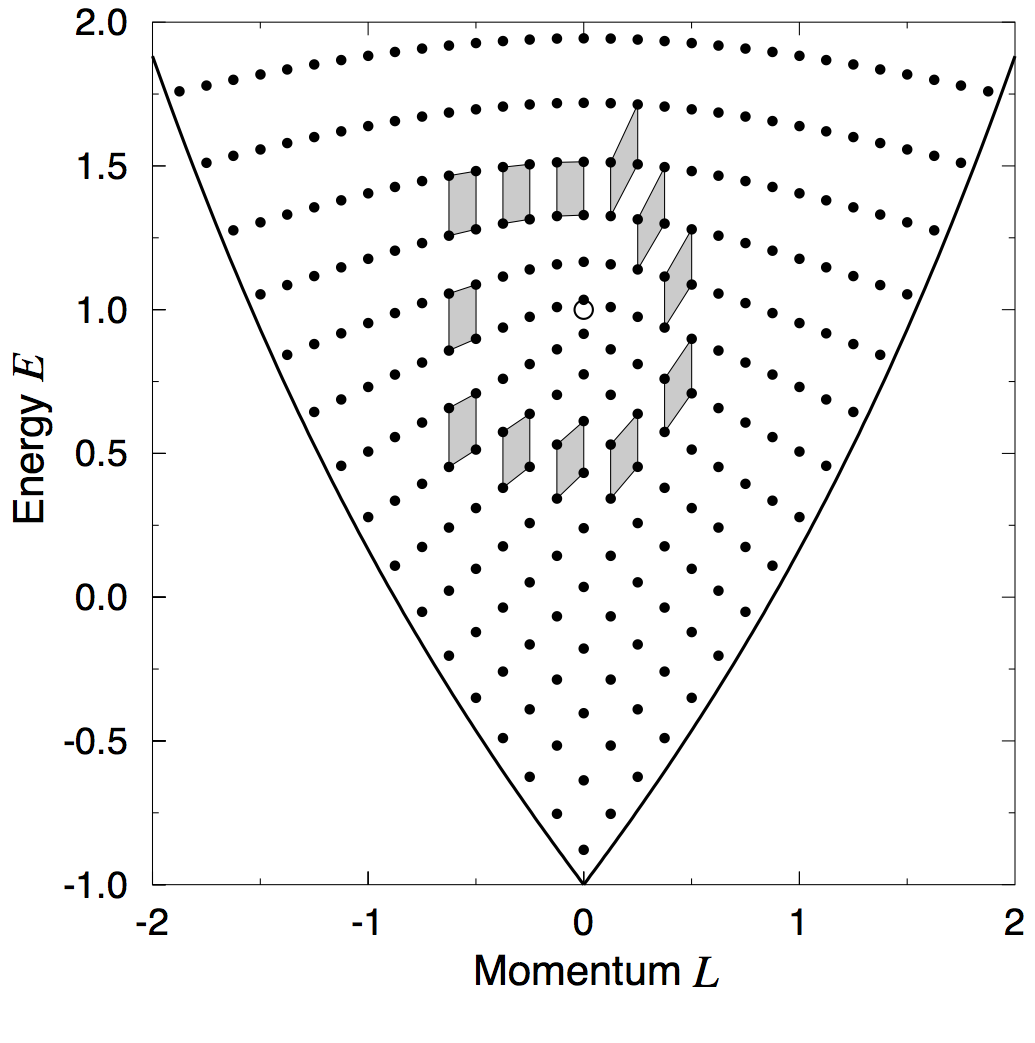
The study of the global geometric properties of physical systems, both at the classical and quantum levels, reveals intriguing geometric structures and explains the structure of the corresponding joint quantum spectra. Here we have only touched on this active field of research in which the group of Dynamical Systems, Geometry, and Mathematical Physics at the JBI is deeply involved.

References

[1] Global aspects of classical integrable systems, 2nd edition. R. H. Cushman and L. M. Bates. Birkhäuser (2015). https://doi.org/10.1007/978-3-0348-0918-4
[2] On global action-angle coordinates. J. J. Duistermaat. Communications on Pure and Applied Mathematics, 33(6):687–706 (1980). https://doi.org/10.1002/cpa.3160330602
[3] Monodromy of Hamiltonian systems with complexity 1 torus actions. K. Efstathiou and N. Martynchuk. Journal of Geometry and Physics, 115:104-115 (2017). https://doi.org/10.1016/j.geomphys.2016.05.014
[4] Monodromy in the hydrogen atom in crossed fields. R. H. Cushman and D. A. Sadovskií. Physica D: Nonlinear Phenomena, 142(1-2):166–196 (2000). https://doi.org/10.1016/S0167-2789(00)00053-1
[5] Defect in the joint spectrum of hydrogen due to monodromy. H. Dullin and H. Waalkens. Arxiv preprint (2016). https://arxiv.org/abs/1612.00823